数学、塾に行って勉強してるんだけど、全然成績が上がらなくて、やる気が起きません…
 女性さん
女性さん塾では勉強してるって言うんですが、家ではまったくやらないんです…!
 寺田
寺田
ひょっとすると、勉強のやり方が間違っているから、やる気が起きないだけかも知れませんよ。
手順を変えれば、解決すると思います!
というようなやりとりが、随分前ですがありました。
一通り解説して、やらせてみしたところ、今まで苦手で勉強する気が起きないと言っていたのに、数学が楽しくなって、自宅でも勉強をやるようになった、とのご報告が。
そうなると、もう当たり前の話なのですが、数学の成績がいきなりジャンプアップしまして、3ヶ月でことのばを卒業してしまいましたとさ。(^^;
]基本的に、ことのばは「3ヶ月程度で卒業してください」というスタンスですので、それでいいんですが。まぁ、塾経営的にはどうなのって話もありますよね。苦笑
学校でも塾でも勉強法を指導してくれない!
今の学校教育の最大の問題は、学校でも塾でも勉強のやり方を教えてくれない、ということ。
算数は指導するけど、算数が得意になるための勉強法も、算数の力が定着するための勉強法も教えてくれません。
ま、うちの息子の通う中学校でも「とにかくノート一杯に英単語を埋めてこい」みたいな、まったく学習効果が得られず、生徒を勉強嫌い、学校嫌いにさせる効果しかなさそうな宿題がわんさかでていますので、そもそも学校の先生も塾の先生も、正しい勉強法を知らないだけって話になるんですけどね。
ちまたには「○○式勉強法」なる書籍やノウハウ集があふれていますが、それは「私がやって役に立った勉強法」、つまり効果の上がったやり方の一事例に過ぎず、それでうまくいく人もいるし、そうでない人の方が多いというのが実情。なぜ、その方法がうまくいくのか、いかないとしたら何が違うのかを理解できないと、自分なりのアレンジもできませんよね。
そういうわけで、ここでは「勉強ができるようになる」あるいは「勉強をやった分だけ、できるようになる」ような勉強法を紹介します。
あくまで基本ですが、最初はこの通りにやってみることをお勧めします。独自性を発揮せず、少なくとも定期考査2回こなすくらいまでは、このやり方でやってみてください。
■勉強の基本原理
(1)学習が成立するには4つのフェーズを越える必要がある
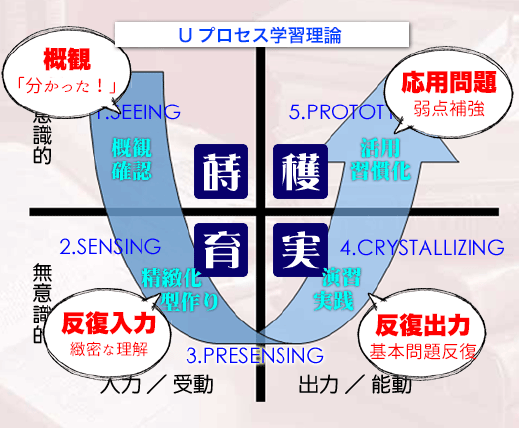
勉強は4つのフェーズを通過して「できる!」状態になります。そして、1つ1つのフェーズは、基本的に前の段階をきちんとこなしていないと、うまくいきません。
もちろん、それぞれのフェーズにどれだけ時間をかけるべきかは、人それぞれ。何度かやりながら、自分なりの最適な時間・労力配分を考えてみてください。
1-1.概観フェーズ
ここは授業を聞いて「分かった」あるいは「分からないことが分かった」ということの確認が必要です。
分からない部分があれば、授業の直後にでも先生に質問するか、帰って参考書をひもとくか、何らかの方法で「とりあえず分かった」状態にする必要があります。
逆に、授業を聞いて分かったからといって、それで安心してはいけません。「分かった」からといって「できる」とは限りませんからね。
あくまで「分かった」は、学習がスタートしたという第一歩に過ぎないのです。
1-2.反復入力のフェーズ
ここは学んだことを「なんとなく分かった」状態から「十分に理解できた」状態に引き上げるフェーズです。
国語や社会なら、テキストを何度も読み込み、十分に理解できている状態を作ります。
数学や理科の物理・化学分野のような計算や証明などが必要な場合であれば、考え方を実際の問題、計算式に適用する方法と手順が十分に理解できたという状態を作ります。
1-3.反復出力のフェーズ
入力を終えたら出力に向かうわけですが、このフェーズが非常に重要な意味を持ちます。
「わかった」を「できる」に換える段階です。
1-2を野球(のバッティング)に喩えるなら「フォームをチェックしながら、無心に素振りをする」フェーズですが、ここは「素振りで身につけたフォームを崩さないように、何度もトスバッティングする」フェーズです。バスケの桜木君が安西先生に連れられて合宿に行き、2万本のシュート練習をしましたが、あんなイメージ。
大事なことは、無心に、ひたすら反復すること。
自分の状態を、内的なフィードバック、客観的な観察によるフィードバック、そして「○本中○本決めた」というような数値などの指標によるフィードバックの3種類をうまく取り入れて、正しい型を身につけていきます。

大切なことは、できている、できていないということをあまり考えず、とにかく体当たりで突き進み、量をこなすこと。
途中のフィードバックを適切に取り入れ、軌道修正を行いながら取り組むこと。
少しずつバリエーションを変え、負荷を上げていくこと。
スムーズにこなせるようになるまで繰り返すこと、です。
1-4.応用問題のフェーズ
今まで取り組んできたことだけでなく、自分が過去に学んだことや、その他様々な思考法を総動員して、1つ1つの課題をクリアしていくフェーズです。
1-3は量をこなすことに意味がありますから、1つ1つに時間をかける必要はありません。しかし、ここでは徹底的に知識と思考力を総動員して解くプロセスに意味がありますので、ある程度の時間をかけて取り組む必要があります。
(2)フェーズによって取り組み方が違う!
以上、4つのフェーズを確認しましたが、それぞれ目的が違いますので、やり方は当然違います。どんな問題に取り組むのかとか、解くのにかける時間の配分とか…
(3)反復は時間をおいて(Spacing Repetition)
学校の先生は「単語を10回繰り返し書け」みたいな「労力をかけるだけの作業」が大好きですが、これは学習効果がほぼゼロです。
単語を100個憶えたければ、1単語ずつ10回書くのではなく、100個をどんどん書いていき(この時は単語を見ながら書いていい)、前に書いたものを見ないで2回目を書いていく…という具合にする必要があります。
最初の学習(見ながら書く)から数分以上経過している必要があります。100個書けば、たいてい数分以上経っているはずなので、続けて2週目に行っても問題ないでしょう。
(4)「想い出す」のに3秒以上かける必要なし!(TOT problem)
計算のやり方だったり、他教科の知識だったりを想い出す時「えーっとえーっと」「あー、出てきそうで出てこない!」となることがあります。
この場合、時間をかけて想い出した方がいいのか? さっさと諦めて答えを確認した方がいいのか?
答えは、見出しにあるように時間をかける必要なし、です。
むしろ時間をかけて想い出そうとしてしまうと、「悩んだ時間」という強烈な体験が記憶されてしまい、肝心な記憶対象を憶えられなくなってしまうのです。
これについては、興味があればこちらの記事をどうぞ。

ということで、原理についてはここまでにしておいて、続いて具体的な方法を解説します。
■実際の復習の進め方
(1)4つのフェーズの位置づけ
原理で説明した4つのフェーズは、次のような位置づけになります。
- 概観=授業:授業を受けた状態がここ
- 反復入力=授業のあった日の夜:学校の宿題+基本問題
- 反復出力=授業のあった週末 or 授業の 3 日後:標準・応用レベルの問題
- 応用問題=試験前:定期考査予想問題集など
(2)使用するテキスト
概観のフェーズは教科書で問題ありません。
教科書の「例題」と「問い」をセットで使うといいですね。(ただし、「問い」の答えが分かっていないといけませんが…)
それ以外は、とりあえず基本・標準・応用の問題が豊富にあれば、どのような問題集でも、問題ありません。
一応、ことのばで使っているテキストをご紹介します。
超基本(基礎)問題集
通称「かっぱ」
※画像をクリックするとAmazonに飛びます。
機械的に解けているけど、どうもリクツとか意味とかを理解してないなと思ったらこちら。
基本から応用まで
通称「3ステップ」
※画像をクリックするとAmazonに飛びます。
骨のある応用問題
通称「ハイクラス」
※画像をクリックするとAmazonに飛びます。
テスト直前に取り組む模擬試験的問題集
通称「定期テスト対策ワーク」
※画像をクリックするとAmazonに飛びます。
(3)実際の取り組み方
3-1.概観のポイント(授業)
- 数学の授業については、予習よりも復習を重視する。
- 授業の内容で「説明が分からなかったところ」と「問題の解き方でつまづいたところ」を、必ずその日のうちに先生に質問・相談して解消しておくこと。
- 自宅学習でこの範囲をやる場合は、
(1)教科書の解き方解説・解答例付き例題を読みながら、解き方を確認する。
(2)例題と同じタイプの問題を解いてみる。分からない場合は、例題の解き方を確認しながら解く。
(3)さらに基本問題を解く。1問ずつ答え合わせをおこない、「一応、解き方が分かった」といえる状態を作る。
3-2.反復入力のポイント(授業のあった日の復習)
- 授業で出された宿題+問題集の基本問題(「とにかく基礎(かっぱ)」と「3 ステップの STEP 1」)で、授業の内容の確認
- もし、分からない問題、すぐに解けない(考え込んでしまう)問題があれば、時間をかけるのではなく(思考時間3秒以内)、チェックを入れて付箋をはった上で次の問題に進む。
- 大問1つ(または小問4問)ごとに答え合わせをおこなう。解けなかった問題、間違えた問題は答えを確認した上で、改めて(答えを見ないで)問題を解き直す(リハーサル)。そこでまた解けなければ、答えを写しながら、教科書の解説と照らし合わせて、解き方や意味を十分に理解する。(付箋はそのまま)
- 1時間以上時間を空けてから付箋の貼ってある問題に再挑戦する(リトリーバル)。ここでもし解けなければ問題と答えを、特別に用意したノートに問題と答えを書き写し、十分理解できる状態にする(リラーニング)。
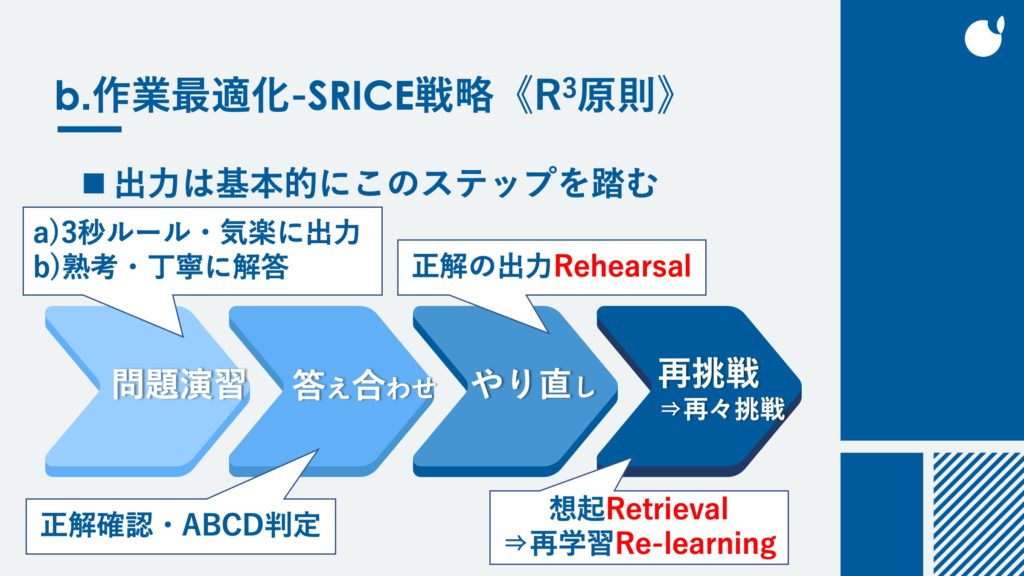
3-3.反復出力のポイント(授業のあった日の3日後、またはその週末)
- 2で付箋を貼った問題を一通り解き直す。スムーズかつ正確に解けることを確認する。スムーズに解け、正解できたら付箋を剥がす。付箋が残った問題は後日再挑戦。(リトリーバル&リラーニング)
- 続いて、3ステップのSTEP2に取り組む。
- 分からない問題、すぐに解けない問題があれば、チェックを入れて付箋をはった上で次の問題に進む。
- 大問2つごとに答え合わせをおこなう。解けなかった問題、間違えた問題は答えを確認した上でチェックと付箋をつけておく。
- 授業の範囲がすべて終わったら、あらためてチェック+付箋の着いた問題を解き直す。解けなかった問題には星印☆を着け、解き方を確認した上で、すべての問題のやり直しが終わったところで再び解き直す。
- STEP2の問題がすべてクリアできたら、STEP3に進む。取り組み方はStep2と同じ。
- 間違えた問題(付箋の着いた問題)の解き直しは2と同じ。
3-4.応用問題のポイント(試験前)
- 3ステップのSTEP2,3のチェックがついた問題を解き直す。(付箋がすべて取り除かれている状態が前提!)
- 解けない問題があれば、ノートに丁寧に解法を書いていく。自分がなぜ間違えたか、何に気をつけるべきかはっきり分かるように書いておく。
- ハイクラス問題に取り組む。1問ずつ丁寧に解く。設問の文章で示される、解くのに必要な情報にアンダーラインを引き、そのアンダーラインの箇所から何が言えるか、どんな式が立てられるかを無作為に書き出す。解けるところまで、がんばって取り組む。
- がんばって考えて「ここまではできたけど、もう無理」と思ったら(時間との兼ね合いも考える)、指導者にヒントをもらう。それでも解けなければ模範解答をノートに書き写し、設問に示されている条件と模範解答がどう対応し、どう解いていけばよかったかを丁寧に確認する。
- 仕上げに「定期テスト対策ワーク」に取り組み、単元ごとに一気に解き進め、自分の苦手なポイント を洗い出す。「スムーズ・スピーディーに解けて、正確に解ける」ことが重要。
以上が、実際にことのばでやらせている学習手順です。
ぜひ、これを参考にして学校の授業、塾の学習の効果を最大限に引き出してください!